Timezone Lookup Revisited
… in which we look at how to really speed up the lookup of geographic locations in a large number or regions covering the entire Earth surface. This is the problem that the tzgeolookup package has to solve: given a geographic location it needs to determine which one among the 425 time zones it belongs to, and it has to do it quickly.
I wrote about time zone lookup previously to cover visualization, the lookup algorithm and storing the lookup data on disk. The original implementation used a “point-in-polygon” test, and would be able to do a lookup in about 15 – 20 milliseconds. This is not too bad, given that the implementation has to check if the given location is inside any of the 1420 polygons which define the 425 time zones. Since most of the time zone polygons have thousands of points (largest one has 152378, but on average there are about 4500 points), this check takes a lot of time. Some optimizations are possible, and they are the topics of the previous posts, but ultimately there is no way of avoiding angle calculations for thousands of data points. With all this optimizations, the original implementation could do a lookup in about 15 – 20 milliseconds, which was sufficient for my needs.
What if you want to do lookups in 1 millisecond or less? This would be a tenfold (10x) improvement over the original implementation, and it cannot be done simply by optimizing the floating point calculations, instead it requires a completely different approach.
I first read about Google’s S2 Geometry library a few years ago and I was impressed by the possibility of building indexes for fast lookup of geographic data. This library allows associating a 64 bit integer with every region on Earth, with the smallest regions that can be indexed being less than 1 cm². Regions that are close to each other geographically have close integer IDs, which allows building indexes from sorted list of IDs.
Here is an overview of the S2 library and what it can do, however, I decided to write my own implementation in Racket, the geoid package. Being a single-person effort, the “geoid” package lacks many of the features of the full S2 library, but I already used it in my ActivityLog2 application for various geographic database queries, such as finding nearby routes for bike rides, elevation correction or building heatmaps.
The latest feature that I added to the “geoid” library is the ability to tile a region, that is determine the list of 64 bit IDs, which cover a region. Since any region can be expressed as a list of integers, determining if a point is inside a region, resolves to finding if an integer is inside a sorted list of other integers — an operation that modern computers can do very quickly. This property comes in handy for looking up the time zone for a specific location, since we can express the entire time zone coverage of Earth as a sorted list of 64 bit integers — this list contains about 5 million integers, but, since the list is sorted, searching through it requires only about 23 integer comparisons.
Tiling Basics
Tiling, that is finding the geoids that cover a region, and the internal workings of the geoid library are too complex to cover in a short blog post, but here is an overview. Below is the tiling of all time zones for Australia, this is done with geoids that cover regions of own to a minimum of 36x36 km — the geoid library can go much smaller than that, but they become more difficult to see on the map.
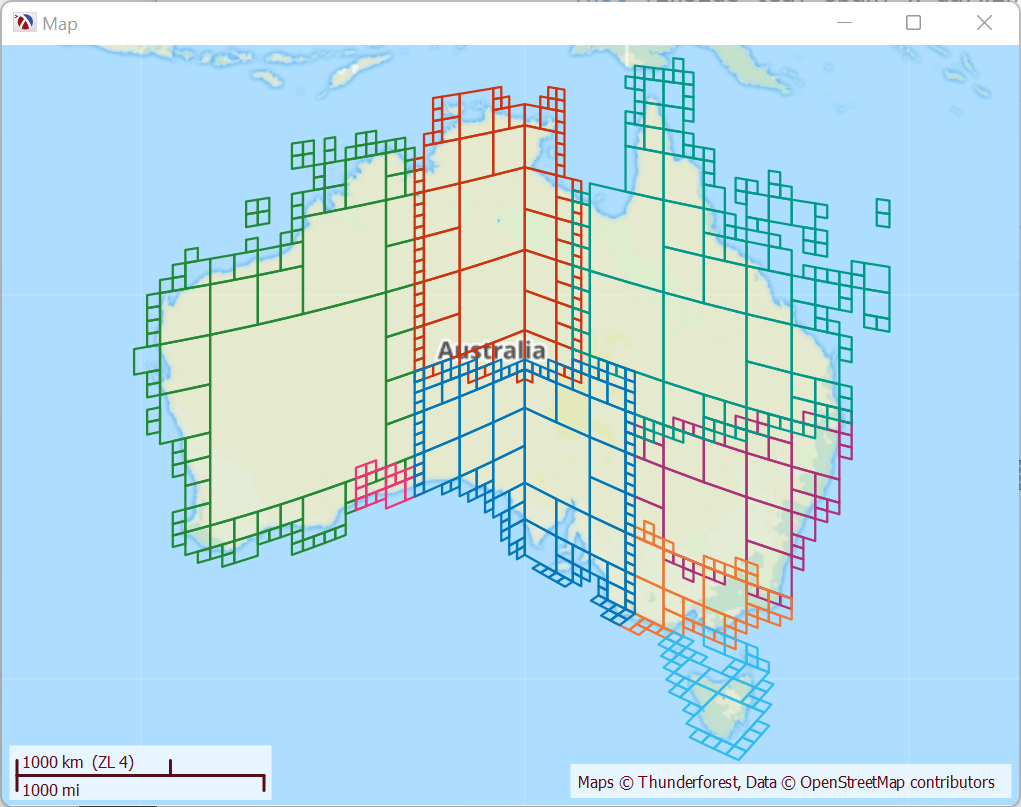
For example, the New South Whales (NSW) region, the purple geoids in the map, is composed of 53 geoids, and, since geoids are ordered and most of them are consecutive, this list can be reduced to only 19 intervals, which are shown below. To find out if a location is inside NSW, we determine its 64 bit ID, than check if the number is inside any of these 19 regions:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
'((7660763703645569025 . 7661045178622279681) (7661185916110635009 . 7662874765970898945) (7701155362803548161 . 7703407162617233409) (7707910762244603905 . 7719310498801385473) (7719591973778096129 . 7720014186243162113) (7720154923731517441 . 7720295661219872769) (7727332535637639169 . 7727614010614349825) (7728176960567771137 . 7728317698056126465) (7728599173032837121 . 7729021385497903105) (7738591534706065409 . 7738732272194420737) (7739435959636197377 . 7744783984193699841) (7746332096565608449 . 7752102333588176897) (7752243071076532225 . 7759842895447719937) (7760124370424430593 . 7760405845401141249) (7762516907726471169 . 7763783545121669121) (7778560981398978561 . 7778701718887333889) (7778842456375689217 . 7779405406329110529) (7785034905863323649 . 7785316380840034305) (7815152728371363841 . 7815434203348074497)) |
For the timezone lookup, tiling for the time zone regions is done down to 70x70 meter geoids, which increases the precision of the lookup but the lists are larger, the package has an 8Mb database at this level of precision. A higher precision is possible, but results in bigger database size.
Distributed Tiling
The tiling for each region has to be pre-calculated from the input data, which is a set of regions defined by a list of coordinates. For small regions or coarse tiling, the duration of the tiling process is short, a few hundred milliseconds, but for detailed tiling of large regions such as time zones that cover the entire world, this can take a very long time. A Racket process running a single thread would take more than 100 hours to produce this data.
The resulting data set can be saved to disk and does not have to be re-computed unless the input data changes, however, while developing the program I had to re-run the process many times so I had to find way to speed it up. The natural solution is to do things in parallel, since the tiling of a region is completely independent of all the others. Racket has places to run multiple processor threads in parallel, but, on my modest 8 core laptop, running 8 tasks in parallel would still take a very long time, so, to further speed things up, the tiling process is designed around a coordinator process which manages the work and stores the data and workers which do the actual work in small chunks. A large number of workers can be distributed on multiple computers and each worker process starts a number of threads corresponding to the number of cores on each computer, thus parallelizing the work.
This process could be distributed on several VMs from one of the Cloud providers out there, but renting VMs for CPU intensive work costs significant amount of money, so I just used the Raspberry PI on my local network to host the coordinator and I borrowed my children’s laptops to help out with the tiling. Here is my home made “computing cluster”:

The process of generating all the timezone regions at 70 meters of accuracy, still takes about 2 hours, but this is more manageable. Also, once the tiling data is generated, the process only has to be repeated when time zones changes, and this happens only a few times a year.
Final Thoughts
With geoids generated and stored in a SQLite database, the [tzgeolookup][tzgeolookup] package implementation for the lookup-timezone function is just over 200 lines of Racket code, most of it dealing with SQL database lookups and caching a few things in memory. The implementation is also about 10 times faster than the previous version, and this performance improvement could not have been achieved just by optimizing the existing code.