A Game of Tetris (gameplay)
.. in which we implement a Tetris game step-by-step in Racket, exploring pict graphics, contracts and unit tests.
If you are not familiar with the Tetris, you can watch a (really bad) game play below. In the game, tiles fall from above and accumulate at the bottom of the playing field and any lines that are completely filled will disappear, and all the accumulated squares will collapse below, making room for more pieces. You can play the game forever, assuming you are skilled enough to match and complete full lines to make them disappear.

Tetris Gameplay
If you are in a hurry, and don’t want to read through the blog post, the final program is available in this GitHub Gist.
In this blog post we’ll build the game from ground up in several increments and we start with the Tetris blocks. Before we begin writing the racket program, we need to put the following at the beginning of the file:
The "#lang racket/gui" defines this as a Racket GUI program, and pict, racket/draw and racket/contract are libraries that are used by the program, while the rackunit library will be used for the unit tests. All these libraries are part of the standard Racket installation.
The Tetris Blocks

The Tetris Blocks
There are seven shapes that make up the set of blocks used in Tetris, all of them fit into a 4x4 grid. The color of the blocks is not important for the game, except that it makes blocks easier to differentiate. The blocks are named using letters which roughly resemble their shape (from left to right): I, Q (from square), L, J, T, Z and S. In Racket, each block can be defined as a list of strings, with the dot (.) character stating for an empty square and a letter standing for a filled in one:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
(define I-Block (define Q-Block (define L-Block (define J-Block '(".I.." '("...." '("LL.." '(".JJ." ".I.." ".QQ." ".L.." ".J.." ".I.." ".QQ." ".L.." ".J.." ".I..")) "....")) "....")) "....")) (define T-Block (define Z-Block (define S-Block '(".T.." '(".Z.." '("S..." "TTT." "ZZ.." "SS.." "...." "Z..." ".S.." "....")) "....")) "....")) (define all-blocks (list I-Block Q-Block L-Block J-Block T-Block Z-Block S-Block)) |
Using a string representation means that there is a visual cue about the shape of the blocks right in the program source. Racket will also display strings directly, so the results of various functions can be inspected directly into the REPL, without the need to define separate functions to display the data structures.
Using lists of strings for our blocks has some disadvantages, since Racket cannot validate a correct block definition. Before we start writing functions which manipulate these blocks, it is useful to define two validation functions, valid-block-row? will check if a single string is valid for a block definition, while valid-block? will verify that a tetris block definition actually conforms to our conventions:
1 2 3 4 5 6 7 8 9 10 |
(define (valid-block-row? row) (and (string? row) ; a row is a string (= (string-length row) 4) ; of 4 characters (for/and ([item (in-string row)]) ; containing only valid characters (and (member item '(#\. #\I #\Q #\L #\J #\T #\Z #\S)) #t)))) (define (valid-block? block) (and (list? block) ; a block is a list (= (length block) 4) ; ... of 4 items (andmap valid-block-row? block))) ; ... each element is a valid row |
Since we wrote some functions, we might as well write tests for them, so we have some confidence that they work correctly. It is also a good idea to test that our functions can detect invalid cases in addition to the valid ones. The test also verifies that our block definitions are actually correct, this means that these blocks can be updated, or new ones added, and the code will automatically check that they are correct (if you run the code in DrRacket, the tests will run automatically):
1 2 3 4 5 6 7 8 9 10 11 12 13 |
(module+ test (check-false (valid-block-row? 1)) ; not a string (check-false (valid-block-row? "......")) ; more than 4 characters (check-false (valid-block-row? "X...")) ; containing invalid characters (check-false (valid-block? "hello")) ; not a list (check-false (valid-block? (append L-Block T-Block))) ; more than 4 items (check-false (valid-block? (list "...." "...." "...." 1))) ; not a list of strings (check-false (valid-block? (list "X..." "...." "...." "...."))) ; contains invalid characters ;; Verify that all our blocks are correctly defined (for ([block (in-list all-blocks)]) (check-pred valid-block? block))) |
Graphics Representation of Blocks
If you have some experience with GUI applications, you would think that we need to construct a frame and a canvas before we can draw the tetris blocks, but in Racket all this can be left until later. We will use the pict package for the graphics and have them displayed directly in the DrRacket REPL.
Blocks can be constructed out of squares, an empty one for the spaces in the 4x4 grid and a color square for the filled in squares. The square-size defines the size of each square, it is useful to define it separately, so blocks can be easily made bigger or smaller. We will also define a mapping from the characters used in block strings to actual colors:
The block->pict function will take a tetris block definition and produce a picture from it. It does that by applying row->squares to each line in the block and appending the resulting pictures using vc-append (which stands for “vertical-center append”. The row->squares function will convert a block row, which is a string, into a picture, with one square for each character in the string. The function looks up the color corresponding to each character and constructs a square of the appropriate color, or an empty one if no corresponding color is found (note that there is no corresponding color for the dot (.) character, which represents the empty space).
1 2 3 4 5 6 7 8 9 10 11 12 13 |
(define/contract (block->pict block) (-> valid-block? pict?) (apply vc-append (map row->squares block))) (define/contract (row->squares row) (-> string? pict?) (define items (for/list ([char (in-string row)]) (define color (hash-ref colors char #f)) (if color (filled-rectangle square-size square-size #:color color) (rectangle square-size square-size)))) (apply hc-append items)) |
Both functions are protected by contracts, as indicated by the define/contract form. This ensures that they will check that their arguments are what we expect them to be (e.g. a valid tetris block for the block->pict function) and they return the expected value, a pict in our case. In addition to tests, contracts are useful in ensuring that defects in the code are detected and reported as early as possible.
The graphics can be inspected directly in the DrRacket REPL, by running (block->pict T-Block) to display a single block, or building a list of these pictures using (map block->pict all-blocks):
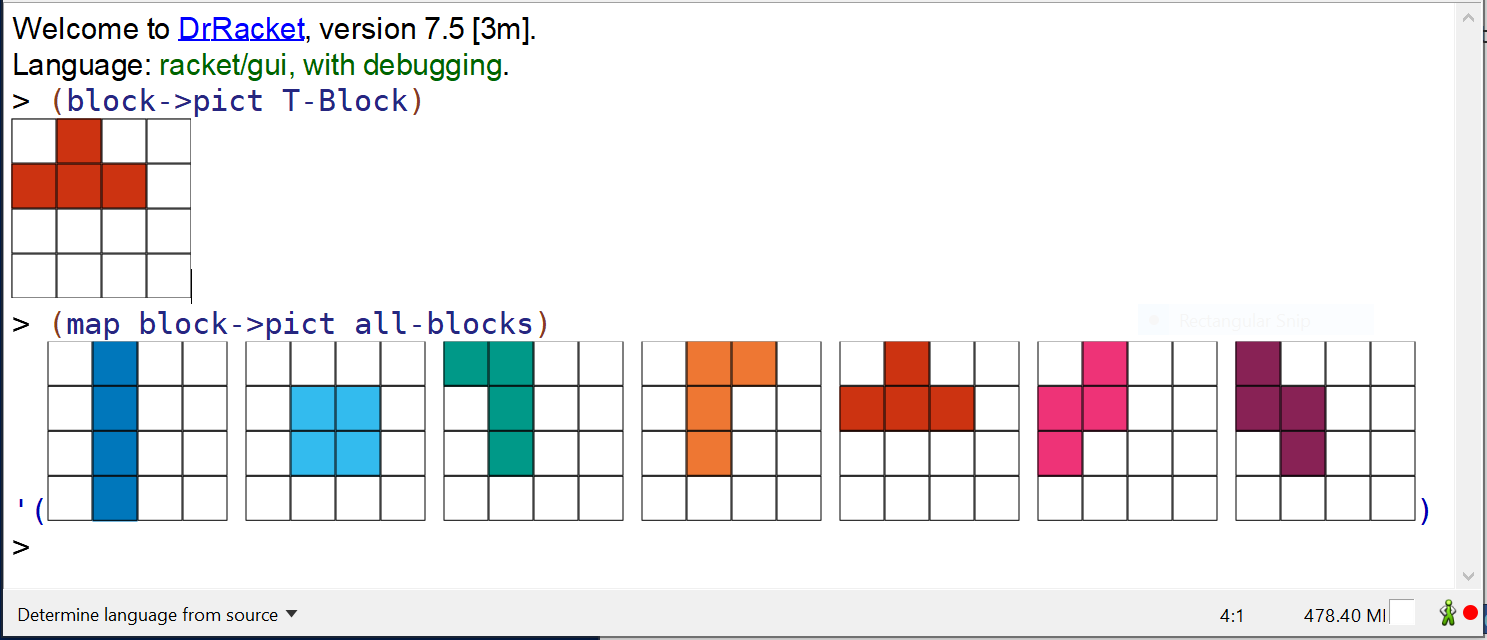
Block Picts in DrRacket REPL
The graphics representation prints out the tetris block using the entire 4x4 grid. This is not desirable in the final game, but it is useful while developing the application, as we can see how each piece aligns with the rest. Once the application is ready, these grid lines can be removed by using the ghost pict constructor on the rectangle one.
Block Rotation
Tetris Blocks And Their Rotations
Blocks can be rotated clockwise and counter clockwise during the game, in 90 degree increments, so we need to implement a mechanism to rotate the blocks. It is not sufficient to just rotate the graphics representation (the pict library provides a rotate drawing adjuster), instead we need to construct new blocks which are rotated. This is needed because the blocks will also be used to determine if they collide with the bottom of the field or other blocks already at the bottom.
Let’s start with the clockwise rotation. To rotate a block clock wise, each column of characters from left to right will become a row from top to bottom. The rotate-clockwise function works by constructing a list of strings (the rows for the new block), where each string has an element from each of the original block’s rows. Note that the function is protected by a contract, which will verify that the parameter that the function receives is a valid block and the values that the function returns are valid blocks too:
Does this function work? Since the graphics representation of blocks is printed directly in the DrRacket REPL, the function can be tested by evaluating forms like: (block->pict (rotate-clockwise L-Block)). It is tedious to check all rotations by typing in the REPL, but the all-rotations helper function will build all the rotations of a block and will allow us to visually inspect them for correctness:
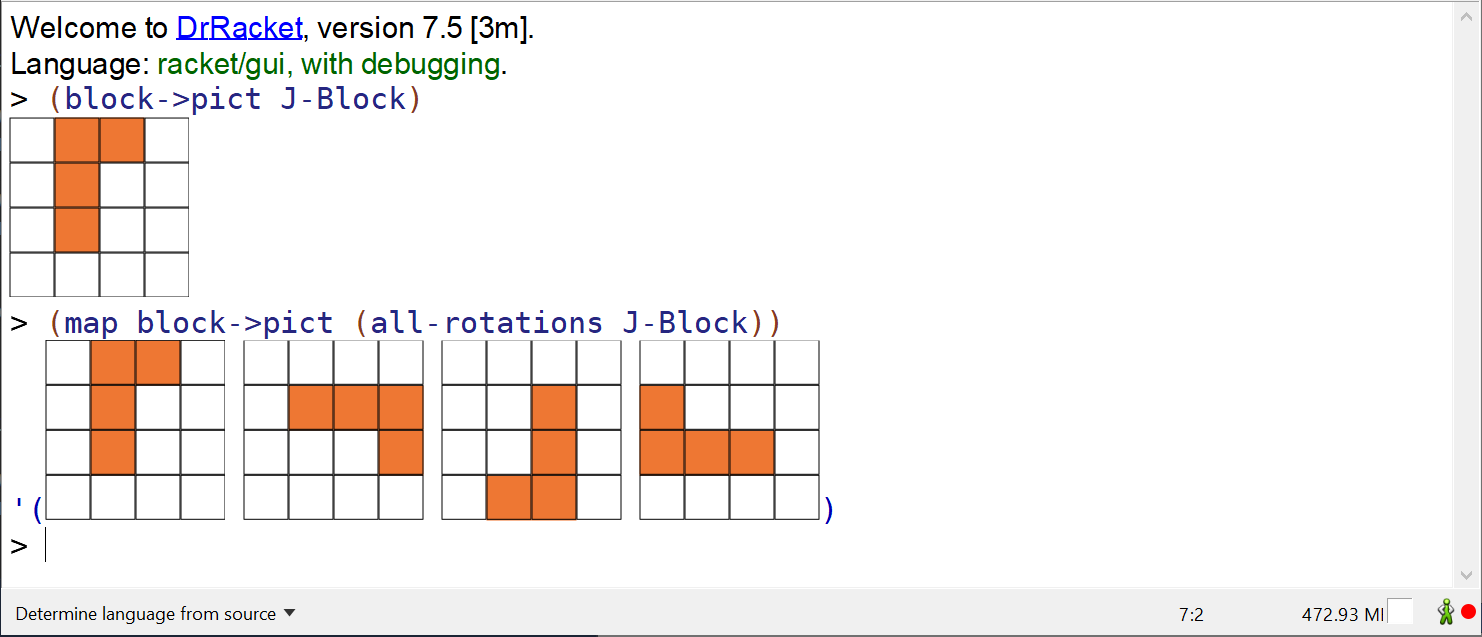
All Rotations of the J Block in the DrRacket REPL
Rotating counter clockwise could also be done using string and list manipulation, but since we already have a function to rotate clockwise, which we now know it works as expected, ca can define counter clockwise rotation simply as rotating a block clockwise 3 times. This is a bit inefficient, but it is fast enough; there will be a discussion on efficiency at the end of this blog post. For now, the aim is to get things working (and working correctly) with a minimum of effort:
1 2 3 4 5 6 7 8 9 10 |
(define/contract (rotate-clockwise* block times) (-> valid-block? exact-nonnegative-integer? valid-block?) (if (> times 0) (let ([rotated (rotate-clockwise block)]) (rotate-clockwise* rotated (sub1 times))) block)) (define/contract (rotate-counter-clockwise block) (-> valid-block? valid-block?) (rotate-clockwise* block 3)) |
We should also add some tests for the new functions. We’ll test that rotating a block clockwise 4 times brings it in the same position and that rotating a block once clockwise once counter-clockwise brings it back into the initial position:
A First Interactive Application
There’s now enough functionality implemented that we can start working on the actual game. To put things together, we need a frame% for the toplevel window, a canvas% to draw the playing field, a timer% to update the game state (which in tetris means making the pieces fall) and some mechanism to read keyboard input from the player and move the pieces.

Falling Blocks with Translation and Rotation
Looking through the Racket GUI, one can easily find the documentation for creating frames, various types of widgets, or timers, but it is not immediately obvious how to handle keyboard input. This is because keyboard input is handled by each individual widget itself, usually by overriding the on-subwindow-char method of a relevant widget. In our case, we need to define a game specific frame class to intercept these keyboard events. tetris-frame% acts like a frame% (which are used for toplevel windows), except it overrides the on-subwindow-char method and passes on the keyboard events to on-tetris-event function, which will be defined later. Note that keyboard events are also passed to the super class, failure to do so would make the application unresponsive to usual keyboard events (the same rule applies for mouse events, but mouse events are not used by this application):
With the tetris-frame% created, the toplevel frame of the game can be instantiated and, at this stage, we need to decide how big the playing field will be. The playing fiel is defined in squares as field-width and field-height, and from these values, the size of the window itself can be determined:
1 2 3 4 5 6 |
(define-values (field-width field-height) (values 12 16)) (define-values (window-width window-height) (values (* field-width square-size) (* field-height square-size))) (define frame (new tetris-frame% [label "Tetris"] [width window-width] [height window-height])) |
We can use a canvas% object to display the game and this class can be used directly. When creating a canvas instance, we need to specify a paint function, which draws onto the canvas. This paint function is automatically invoked when the canvas needs to be updated, or a program can request an update by sending the canvas a refresh message. The paint function will currently display the current block at its location. In the application we will use the “square coordinates”, i.e the dimensions of a bloc are 4x4, but pixels are used when drawing, so the coordinates need to be converted to pixels — this is done by simply multiplying the coordinates by square-size. The draw-pict function is used to draw a pict onto the canvas:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
(define-values (current-block block-x block-y) (values L-Block 0 0)) (define (on-tetris-paint canvas dc) (send dc clear) (define x (* block-x square-size)) (define y (* block-y square-size)) (draw-pict (block->pict current-block) dc x y)) (define canvas (new canvas% [parent frame] [min-width window-width] [min-height window-height] [stretchable-width #f] [stretchable-height #f] [paint-callback on-tetris-paint])) |
Tetris pieces will fall at a constant speed, and this can be achieved using a timer% which will invoke the on-tetris-tick function at regular intervals. This function will increment the Y position of the current block, and, if the Y position is larger than the field height (meaning that the piece is now below the field), it will create a new block by calling spawn-new-block. Changing the interval of the timer will make pieces fall slower or faster — in the real game the pieces start falling faster as the game progresses, but here we just use a constant value of 500 milliseconds. Note that the canvas is refreshed at the end of on-tetris-tick, so the updated game state is reflected on the canvas.
spawn-new-block assigns a new block to current-block and sets the coordinates to the top of the field again. For now, this function just rotates through all blocks, so we can test each one in turn, but in the real game, blocks will be randomly selected:
Keyboard event handling is done in on-tetris-event, which is called from the frame’s on-subwindow-char when a key is pressed. Left and right keys move a piece left or right by adjusting the X position of the block, while the up and down keys rotate the piece clockwise or counter-clockwise by updating the block itself. Note that the canvas is refreshed at the end, so the updated game state is reflected on the canvas.
1 2 3 4 5 6 7 8 9 10 11 12 13 |
(define (on-tetris-event event) (case (send event get-key-code) ((left) (on-left-right-move sub1)) ((right) (on-left-right-move add1)) ((up) (on-rotation rotate-clockwise)) ((down) (on-rotation rotate-counter-clockwise))) (send canvas refresh)) (define (on-rotation rotate-function) (set! current-block (rotate-function current-block))) (define (on-left-right-move direction) (set! block-x (direction block-x))) |
The last part is a function to start a new game: it spawns a new block, gives the keyboard focus to the canvas and shows the toplevel frame:
You can find all the function written so far in this GitHub Gist, you can load it in DrRacket and experiment with it. The program so far shows the game mechanics, but it is still far from a complete game: pieces can be moved outside the field and back in and they don’t accumulate at the bottom. We’ll address those tasks next.
Keeping Blocks Inside the Playing Field
To keep blocks inside the playing field, we need two pieces of functionality: (1) a mechanism to determine if a position is still inside the playing field, which will be used to determine if a piece can be moved left or right, and (2) a mechanism to adjust the position of a piece, to move it back inside the playing field when the piece goes outside because it is rotated. For example, the user is allowed to rotate a vertical I-Block and the block will still remain inside the playing field.
We can write the function inside-playing-field? to test if the block is inside. The function receives the block and the coordinates as parameters, even though the current block and its position is available as a global variable. This is because we need to test if a new position is still inside before updating the global state. The function makes use of a block-bounding-box helper, since we must allow the empty parts of the block to go outside the playing field, so we cannot just test that the 4x4 block is outside.
Perhaps the most complex function so far is block-bounding-box, which determines the coordinates of the actual piece inside the 4x4 block. The function determines the minimum and maximum X and Y values and returns them as four values:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
(define/contract (block-bounding-box block) (-> valid-block? (values integer? integer? integer? integer?)) (define-values (min-x max-x) (for/fold ([min-x 3] [max-x 0]) ([row (in-list block)]) (define row-min-x (for/first ([(item position) (in-indexed (in-string row))] #:unless (equal? #\. item)) position)) (define row-max-x (for/last ([(item position) (in-indexed (in-string row))] #:unless (equal? #\. item)) position)) (values (if row-min-x (min min-x row-min-x) min-x) (if row-max-x (max max-x row-max-x) max-x)))) (define min-y (for/first ([(row position) (in-indexed (in-list block))] #:unless (equal? row "....")) position)) (define max-y (for/last ([(row position) (in-indexed (in-list block))] #:unless (equal? row "....")) position)) (values min-x min-y max-x max-y)) |
This is a complex function, so can we know that it works correctly? Well, we can prove it by test: since there are only 28 possibilities, (7 blocks, 4 rotations each), we can visually look at every combination, and write a test for it:
1 2 3 4 5 6 7 8 9 10 |
(module+ test (define (bb-helper block rotations) (call-with-values (lambda () (block-bounding-box (rotate-clockwise* block rotations))) list)) (check-equal? (bb-helper I-Block 0) '(1 0 1 3)) (check-equal? (bb-helper I-Block 1) '(0 1 3 1)) (check-equal? (bb-helper I-Block 2) '(2 0 2 3)) (check-equal? (bb-helper I-Block 3) '(0 2 3 2)) ;; ... ) |
To keep the length of this blog post in check, the above code omits most of the tests. The final application (see link below) contains the full set of tests, along with tests for inside-playing-field? and adjust-x-position.
The adjust-x-position is used to move a block left or right if it is outside the playing field, and it is used to move pieces that have been rotated back into the playing field:
1 2 3 4 5 6 7 8 9 10 |
Updating the Application
To make use of the new functionality, we need to update the on-left-right-move and on-rotation functions: on-left-right-move will check if the new X position is still inside the playing field, and will only update block-x if it is, while on-rotation will check if the block falls outside after the rotation and bring it back inside the playing field:
1 2 3 4 5 6 7 8 9 |
(define (on-left-right-move direction) (define new-x (direction block-x)) (when (inside-playing-field? current-block new-x block-y) (set! block-x new-x))) (define (on-rotation rotate-function) (set! current-block (rotate-function current-block)) (unless (inside-playing-field? current-block block-x block-y) (set! block-x (adjust-x-position current-block block-x block-y)))) |
This is all that is needed to keep the blocks inside the playing field, next we’ll look into making blocks accumulate at the bottom of the field. You can find the updated program at this GitHub Gist.

Blocks Staying Inside the Playing Field
Accumulating Blocks at the Bottom
When a falling piece reaches the bottom of the playing field, it stops there and it does not simply disappear. The next piece will stop on top of the first one and so on. The “filled” part at bottom part of the field cannot be represented as a collection of blocks, since lines can collapse, leaving partial blocks. Still, we can borrow from the block representation and represent the filled part as a list of strings, each string representing a single row, with characters representing colored blocks. We can even re-use the row->squares function to prepare the pictures for the lines. Unlike blocks, lines will not be defined by us, but created by the program, as the game progresses. Still, it is useful to have some sample data to experiment with:
1 2 3 4 5 |
(define sample-filled-lines '("...........I" "LJJJ...J...I" "LZZJ.SSJ.T.I" "LLZZSSJJTTTI")) |
The above lines might be harder to visualize than the basic tetris blocks, so let’s build a function that constructs a pict out of this data structure:
1 2 3 |
(define/contract (filled-lines->pict lines) (-> (listof valid-filled-line?) pict?) (apply vc-append (map row->squares lines))) |
Just as with blocks, it is useful to define a function which checks if a string is a valid filled line. The full program also has tests for all these functions, but they are omitted from this blog post:
With filled-lines->pict it is now easy to visualize how the filled lines look like:
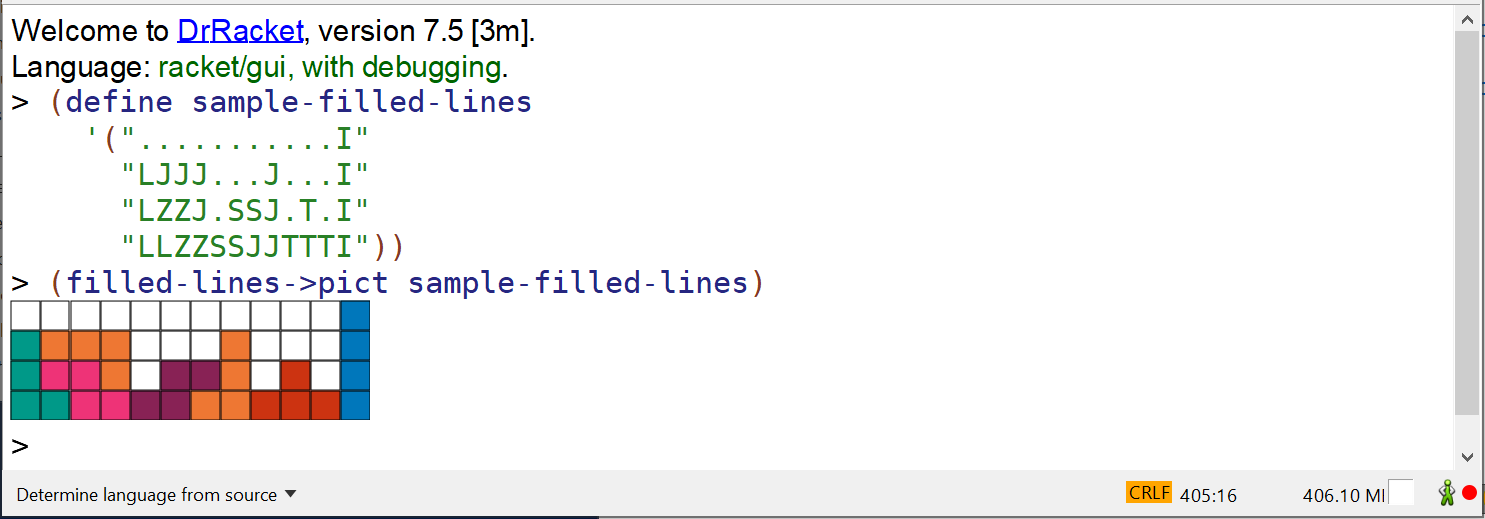
Inspecting Filled Lines in DrRacket REPL
There are two operations that we need to implement: detecting if a block collides with the existing filled lines, and merging a block into the filled lines. These are relatively complex operations, so we’ll define some helper functions first.
A row of a Tetris block is a four character string, while a filled line is a string having field-width characters (12 in this example). Since we need to combine blocks with filled lines, we need a function which expands a four character block row into a filled line, this is done by appending the dot (.) character representing the empty space to the front and back of the block row, according to its X position on the field:
1 2 3 4 5 6 7 8 9 |
(define/contract (block-row->filled-line row x-position) (-> valid-block-row? integer? valid-filled-line?) (define limit (+ x-position (string-length row))) (define items (for/list ([pos (in-range field-width)]) (if (or (< pos x-position) (>= pos limit)) #\. (string-ref row (- pos x-position))))) (apply string items)) |
There is a unit test suite for this function, but here are just some examples:
Another helper function is merge-lines which combines the colored squares from two lines producing a new line. The function will avoid merging a square position where both lines have a colored squares and report an error:
1 2 3 4 5 6 7 8 9 |
(define/contract (merge-lines line1 line2) (-> valid-filled-line? valid-filled-line? valid-filled-line?) (define items (for/list ([a (in-string line1)] [b (in-string line2)]) (cond ((equal? a #\.) b) ((equal? b #\.) a) (#t (error (format "Line collision: ~a vs ~a" line1 line2)))))) (apply string items)) |
Here is some sample use of this function:
merge-lines will raise an error if squares on the two lines collide, but sometimes it is useful to be able to test if two lines collide, without raising an error. block-row-with-line-collision? is such a function: it wraps merge-lines, traps the and just returns #t if merging cannot happen. The result from merge-lines is also discarded and the function just returns #f if there is no merge failure — no merge failure means that the block row does not collide with the line:
1 2 3 4 5 6 7 |
(define/contract (block-row-with-line-collision? block-row x line) (-> valid-block-row? integer? valid-filled-line? boolean?) (define bline (block-row->filled-line block-row x)) (with-handlers ((exn:fail? (lambda (e) #t))) (merge-lines bline line) #f)) |
To check that a Tetris Block, which is a list of rows collides with a set of filled lines, which is a list of strings representing each line, we need to recursively check that each row collides with the filled line at the same Y coordinate. The block-collision? does that, making sure that the block rows and filled lines are matched up based on their Y position. The function has unit tests (and it is complex enough to need them), but they are not showed here.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
(define/contract (block-collision? block x y filled-lines) (-> valid-block? integer? integer? (listof valid-filled-line?) boolean?) (let loop ([bdepth y] [block block] [fdepth (- field-height (length filled-lines))] [filled filled-lines]) (cond ((or (null? block) (null? filled)) #f) ((< bdepth fdepth) (loop (add1 bdepth) (cdr block) fdepth filled)) ((> bdepth fdepth) (loop bdepth block (add1 fdepth) (cdr filled))) (#t (if (block-row-with-line-collision? (car block) x (car filled)) #t (loop (add1 bdepth) (cdr block) (add1 fdepth) (cdr filled))))))) |
Merging blocks is very similar to block-collision? in that block rows and filled lines are paired up and merged, the added complication here is that new lines might have to be created — the simplest example is when a block is merged onto an empty set, when the playing field is initially empty:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
(define empty-line (make-string field-width #\.)) (define (maybe-add line result) (if (and (equal? line empty-line) (null? result)) result (cons line result))) (define (merge-block block x y filled-lines) (let loop ([bdepth y] [block block] [fdepth (- field-height (length filled-lines))] [filled filled-lines] [result '()]) (cond ((< bdepth fdepth) ;; Block row is above filled lines, create new filled lines at the ;; top. (let ([line (block-row->filled-line (car block) x)]) (loop (add1 bdepth) (cdr block) fdepth filled (maybe-add line result)))) ((> bdepth fdepth) ;; Filled lines are above the block row, just add them to the ;; result, no merging is needed (loop y block (add1 fdepth) (cdr filled) (cons (car filled) result))) ((>= fdepth field-height) ;; Filled lines depth is now greater than the field depth -- we're ;; done. (reverse result)) ((null? block) ;; We're done with the block rows, just add the remaining filled ;; lines (loop (add1 bdepth) block (add1 fdepth) (cdr filled) (cons (car filled) result))) (#t ;; The block row is at the same level as a filled line. Merge ;; them, to create a new line (let* ([bline (block-row->filled-line (car block) x)] [line (merge-lines (car filled) bline)]) (loop (add1 bdepth) (cdr block) (add1 fdepth) (cdr filled) (maybe-add line result))))))) |
Updating the Application
We can now update the interactive application to add support for filling lines at the bottom, rather than just discarding the blocks. First, we need to track the filled lines, in addition to the current block, as part of the program state, and start-game will need to initialize this state correctly (since start-game can be called multiple times, to re-start a game):
Next, we need to update spawn-new-block to merge the previous block into the filled lines. Since the playing field is now filling up, the “end of game” condition also needs to be handled, this is where a new block can no longer be spawned as it would immediately collide with the filled lines. The current-block will be set to #f when this occurs, and all the other functions will need to check this, they can no longer assume that current-block is always a tetris block.
1 2 3 4 5 6 7 8 9 10 11 12 13 |
(define (spawn-new-block) (when current-block (set! filled-lines (merge-block current-block block-x block-y filled-lines))) (set! block-count (add1 block-count)) (set! current-block (list-ref all-blocks (modulo block-count (length all-blocks)))) (set! block-y 0) (set! block-x (exact-truncate (- (/ field-width 2) 2))) ;; Playing field is full. Game Over. (when (block-collision? current-block block-x block-y filled-lines) (set! current-block #f))) |
The on-tetris-tick function will now need to check for collisions before moving a block down:
1 2 3 4 5 6 7 8 9 10 |
(define (on-tetris-tick) (when current-block ; will be #f at the end of the game (define inside? (inside-playing-field? current-block block-x (add1 block-y))) (define collision? (block-collision? current-block block-x (add1 block-y) filled-lines)) (if (and inside? (not collision?)) (set! block-y (add1 block-y)) (spawn-new-block)) (send canvas refresh))) |
The on-tetris-paint function will need to also paint the filled lines, this means just using filled-lines->pict and displaying the pict at the correct location:
1 2 3 4 5 6 7 8 9 10 11 |
(define (on-tetris-paint canvas dc) (send dc clear) (unless (null? filled-lines) (define depth (* (- field-height (length filled-lines)) square-size)) (draw-pict (filled-lines->pict filled-lines) dc 0 depth)) (when current-block ; will be #f at the end of the game (define x (* block-x square-size)) (define y (* block-y square-size)) (draw-pict (block->pict current-block) dc x y))) |
The on-tetris-event will need to handle the case when the current-block is #f, and the functions that rotate and move blocks need to be updated to check if the new block position would collide with the filled lines:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
(define (on-tetris-event event) (when current-block ; will be #f at the end of the game (case (send event get-key-code) ((left) (on-left-right-move sub1)) ((right) (on-left-right-move add1)) ((up) (on-rotation rotate-clockwise)) ((down) (on-rotation rotate-counter-clockwise))) (send canvas refresh))) (define (on-rotation rotate-function) (define candidate (rotate-function current-block)) (define-values (min-x min-y max-x max-y) (block-bounding-box candidate)) (cond ; rotating the block would make it collide, don't change it ((block-collision? candidate block-x block-y filled-lines) (void)) ;; rotating the block would make it go below the field bottom, don't ;; change it. ((>= (+ block-y max-y) field-height) (void)) (#t (define x (adjust-x-position candidate block-x block-y)) ;; Bringing the block inside the playing field might make it collide, so ;; we need to check again for collisions. (unless (block-collision? candidate x block-y filled-lines) (set! current-block candidate) (set! block-x x))))) (define (on-left-right-move direction) (when (and (inside-playing-field? current-block (direction block-x) block-y) (not (block-collision? current-block (direction block-x) block-y filled-lines))) (set! block-x (direction block-x)))) |
The application now starts to resemble a Tetris game, and you can find it in this GitHub Gist. If you got this far into the blog post, the remaining parts are easy, so there is no reason not to complete it.

Accumulating Blocks at the Bottom of the Play Field
Collapsing the Complete Lines
The last task for a complete Tetris game is to remove the completed lines from the playing field. A line is complete if it contains no empty squares, which are represented by the dot (.) character:
With full-line? written, the completed lines can be “collapsed” simply by removing them from the list of filled lines:
As with other functions in this blog posts, these functions have tests associated with them, which you can check out in the completed application, linked below.
Completing the Application
The only update is to the spawn-new-block which will remove filled lines after a block is merged. Since the game is now complete, spawn-new-block has also been updated to pick a random piece from the list of blocks, instead of cycling through the blocks:
1 2 3 4 5 6 7 8 9 10 11 |
(define (spawn-new-block) (when current-block (set! filled-lines (merge-block current-block block-x block-y filled-lines)) (set! filled-lines (remove-full-lines filled-lines))) (define candidate (random (length all-blocks))) (set! current-block (list-ref all-blocks candidate)) (set! block-y 0) (set! block-x (exact-truncate (- (/ field-width 2) 2))) ;; Playing field is full. Game Over. (when (block-collision? current-block block-x block-y filled-lines) (set! current-block #f))) |
So there it is, a Tetris game implemented in about 700 lines of Racket code, together with comments and unit tests. You can find the final program in this GitHub Gist. The program is still missing several features that would make it a user friendly game, perhaps the most important one is that it does not keep score. This, and other aspects will be discussed in a future blog post.
Collapsing Completed Lines
Final Thoughts
If you are an experienced programmer, you may have noticed that the implementation presented here is very inefficient. The chosen implementation favored simplicity and validation (to catch defects early) as much as possible. Unfortunately, simplicity and verification are usually done at the expense of performance. Let’s see what the performance problems are:
-
the
valid-block?function is inefficient: it scans a full list and scans each string inside this list looking for characters in another list. -
this
valid-blockis used in a lot of function contracts, so it is called all the time to verify arguments and return values, even though “we know” that the program is correct. -
rotate-clockwiseconstructs new strings and lists every time it is called, and has a contract on it. -
rotate-counter-clockwiseis worse: it callsrotate-clockwisethree times than discards two intermediate results. Contracts are also checked on each intermediate calls. -
every time we display something, a pict is created, either by
block->pictorfilled-lines->pict, the pict object is drawn on the canvas, than discarded. -
did I mention that all functions have contracts which call inefficient functions?
This program is fast enough for a Tetris game, but since most programmers are worried about performance, it is worth discussing it here. What would you do if the program would indeed need a performance boost?
The firsts reaction is to address the immediate problem: contracts are slow, so we disable them. After all, “we know” that the program is correct and nobody wants a slow program. Perhaps you would also try to implement rotate-counter-clockwise more efficiently, struggling with some list and string manipulation. But sometimes, it is worth taking a step back and looking at the big picture. And in the case of Tetris, the big picture is very small indeed, here is in its entirety:
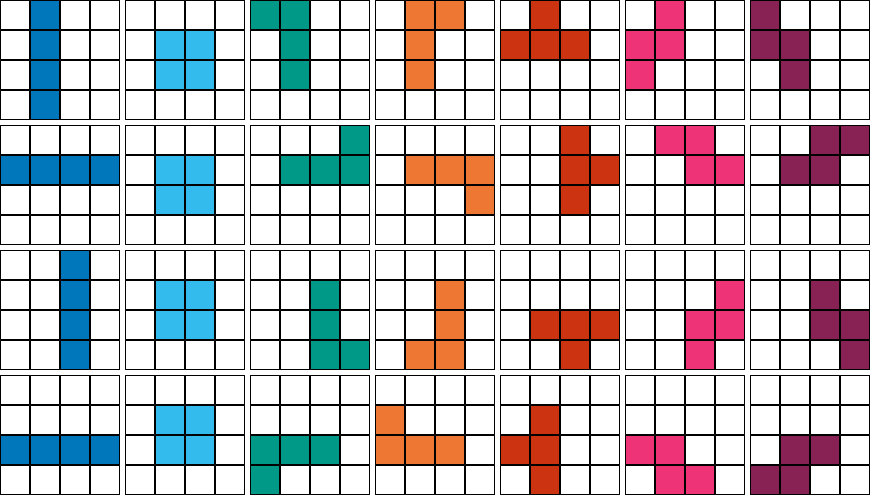
Tetris Blocks and Their Rotations
The key observation is that there are only 28 possible combinations for all the Tetris blocks. This means that all block rotations can be pre-calculated, together with the pict corresponding to each one as well as the bounding box for collision checks. To implement block rotations, all we would have to to is move up and down in the table. To draw the blocks we simply keep the current pict around until we need it. Even filled lines only change when a block is merged, so a pict for them can be pre-calculated. This type of optimization would be many times faster than the best you could achieve by removing contracts or hand optimizing code, and you still get to keep the simplicity and verification code. Something to think about.